Vector Commitments
A vector commitment is simply a Merkle tree. It is configured with two fields:
height: the height of the Merkle treen_verifier_friendly_commitment_layers: the depth at which layers will start using the verifier-friendly hash.
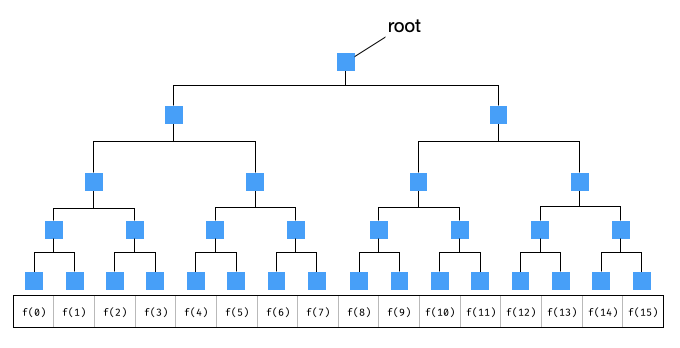
Merkle tree polynomial commitments provide a standard on how to commit to a polynomial using a Merkle tree.
draft
Commitments of polynomials are done using Merkle trees. The Merkle trees can be configured to hash some parameterized number of the lower layers using a circuit-friendly hash function (Poseidon).
hades_permutation(s1, s2, 2) always setting the last field element to MONTGOMERY_R = 3618502788666127798953978732740734578953660990361066340291730267701097005025. The Montgomery form of .
A vector commitment is simply a Merkle tree. It is configured with two fields:
height: the height of the Merkle treen_verifier_friendly_commitment_layers: the depth at which layers will start using the verifier-friendly hash.

A table commitment in this context is a vector commitment where leaves are hashes of multiple values. Or in other words, a leaf can be seen as a hash of a table of multiple columns and a single row.
It can be configured with two fields:
n_columns: the number of columns in each leaf of the treevector: the vector commitment configuration (see previous section).A few examples:
Note that values are multiplied to the MONTGOMERY_R constant before being hashed as leaves in the tree.
TODO: explain why montgomery
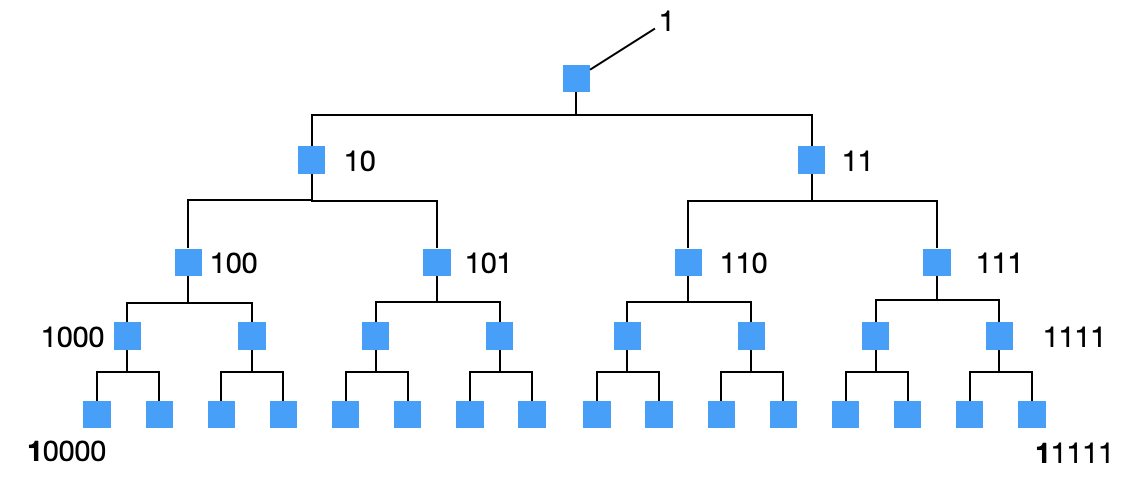
Random evaluation of the polynomial might produce an index in the range with the height of the tree. Due to the way the tree is indexed, we have to convert that index into a path. To do that, the index is added with the value to set its MSB.
For example, the index 0 becomes the path 10000 which correctly points to the first leaf in our example.
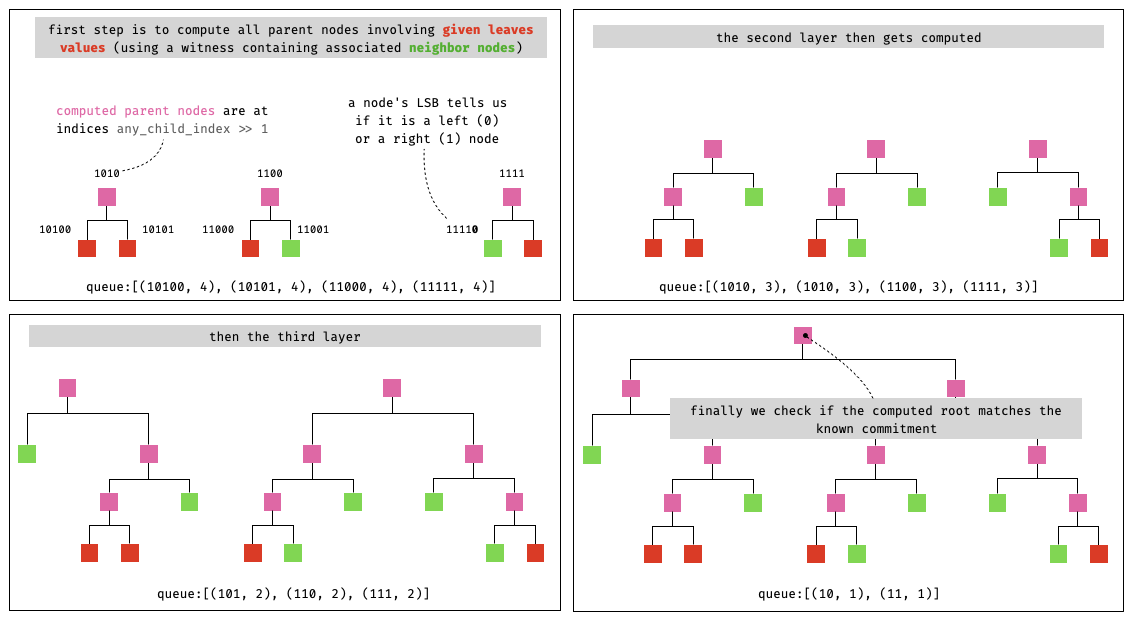
A vector decommitment/membership proof must provide a witness (the neighbor nodes missing to compute the root of the Merkle tree) ordered in a specific way. The following algorithm dictates in which order the nodes hash values provided in the proof are consumed:
A n_verifier_friendly_layers variable can be passed which dictates at which layer the Merkle tree starts using a verifier-friendly hash.
In the following example, the height of the table commitment is (and the height of the vector commitment is ). As such, a n_verifier_friendly_layers of would mean that only the table would use the verifier-friendly hash. A n_verifier_friendly_layers of would mean that the last / bottom layer of the Merkle tree would also use the verifier-friendly hash. A n_verifier_friendly_layers of would mean that all layers would use the verifier-friendly hash.
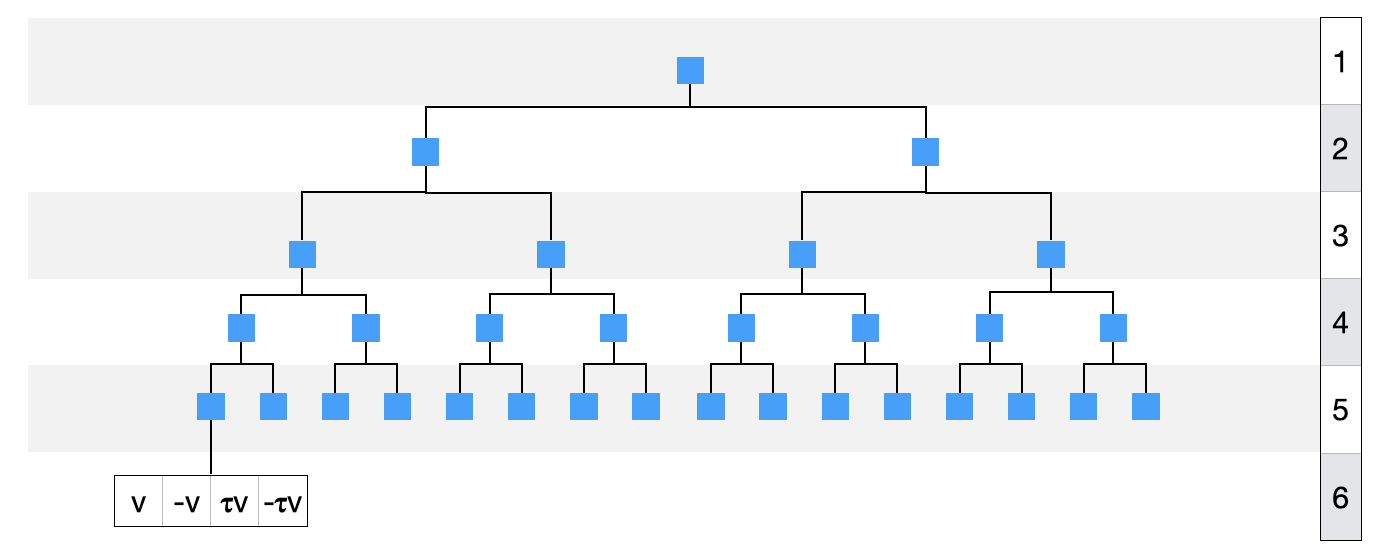
As can be seen in the previous diagram, a leaf can contain (using the technique in table commitments) multiple evaluations of the same polynomial at different points. This is useful for the FRI layer commitments where the same polynomial is evaluated at and (and potentially more values depending on skipped layers).