Overview
In this section we give a brief overview of the Starknet STARK protocol. While the protocol used is designed to verify Cairo programs, we provide an agnostic specification. The instantiation of this protocol with Cairo should be the object of a different specification.
Before we delve into the details, let's look at the protocol from a high-level protocol diagram point of view. The Starknet STARK protocol is divided in three main phases:
- Construction of an interactive arithmetization. In this phase the prover commits to different parts of the execution trace it wants to prove, using random challenges in-between.
- Aggregation of constraints into a composition polynomial. In this phase the prover commits to a composition polynomial that, if checked by FRI, proves that the execution trace satisfies the constraints. It also produces evaluations of commitments at a random point so that the verifier can check that the composition polynomial is well-formed.
- Aggregation of FRI proofs and FRI protocol. The composition polynomial FRI check as well as evaluation proofs (using FRI-PCS) of all the sent evaluations are aggregated into a single FRI check. The FRI protocol is then run to verify the aggregated FRI proof. See the Starknet FRI Verifier specification for more details.
We illustrate the flow in the following diagram:
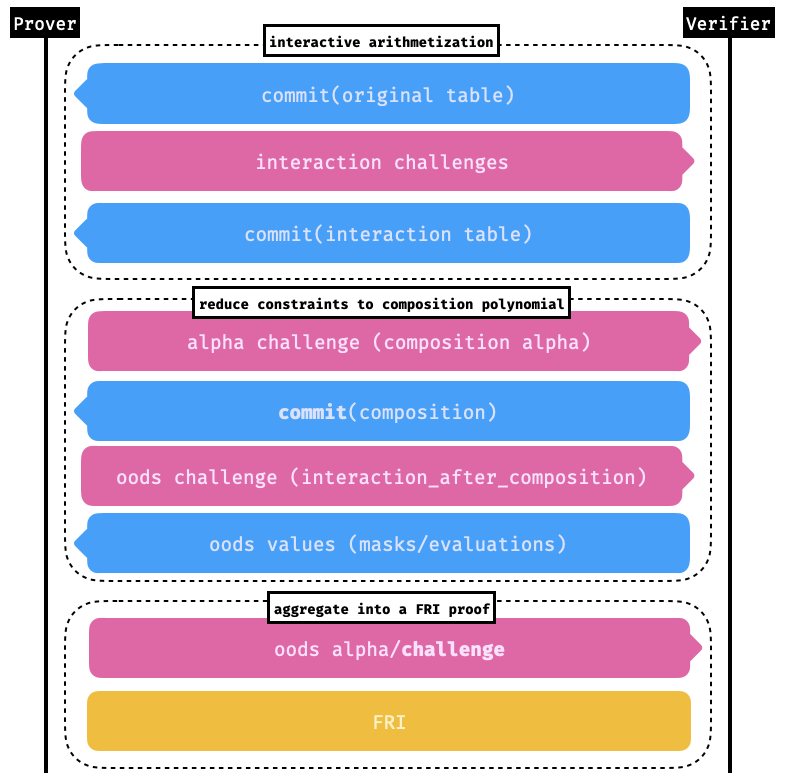
In the next sections we review the different phases.
Interactive AIR Arithmetization
But first, we quickly remind the reader that the Starknet STARK protocol allows a prover to convince a verifier that an AIR (Algebraic Intermediate Representation) arithmetization is satisfied by their witness. This is generally augmented to also include a public input, usually via a public memory extension.
AIR is essentially two things:
- an indexed table representing the execution trace of a run, where columns can be seen as registers and the rows the values they take as one steps through a program. The table takes values when a prover tries to prove an execution.
- a list of fixed constraints that are agreed on.
The indexing of the table is chosen as the elements of the smallest subgroup of power that can index the table.
Furthermore, the columns of a table can be grouped, which allows the prover to fill the table group by group, using challenges from the verifier in-between. This is useful in order to perform an interactive arithmetization where parts of the encoded circuit need verifier randomness to be computed.
We give the example of two "original" columns and one "interaction" column, indexed using the multiplicative subgroup of the 16-th roots of unity:
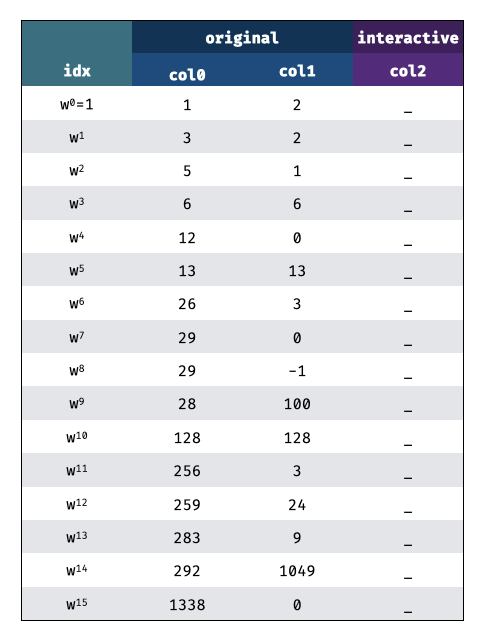
The first phase of the Starknet STARK protocol is to iteratively construct the trace tables (what we previously called interactive arithmetization). The prover sends commitments to parts of the table, and receives verifier challenges in between.
- TODO: we should make this part agnostic to Cairo though.
Composition Polynomial
The role of the verifier is now to verify constraints of the form of polynomials on the trace column polynomials, applied on a domain (a list of all the indexes on which the constraint applies).
As with our example above, we can imagine a list of constraints that need to vanish on a list of associated domains described by their domain polynomials .
By definition, this can be reduced to checking that you can write each as for some quotient polynomial of degree .
While protocols based on polynomial commitments like KZG would commit to the quotient polynomial and then prove the relation at a random point (using Schwartz-Zippel), the Starknet STARK protocol uses a different approach: it uses a FRI check to prove that the commitment to the evaluations of correctly represents a polynomial of low degree.
As such, the role of the verifier is to verify that all the quotient polynomials associated with all the constraints exist and are of low-degree.
TODO: define low-degree better
As we want to avoid having to go through many FRI checks, the verifier sends a challenge which the prover can use to aggregate all of the constraint quotient polynomials into a composition polynomial .
This composition polynomial is quite big, so the prover provides a commitment to chunks or columns of the composition polynomials, interpreting as .
Finally, to allow the verifier to check that has correctly been committed, Schwartz-Zippel is used with a random verifier challenge called the "oods point". Specifically, the verifier evaluates the following and check that they match:
- the left-hand side
- the right-hand side
Of course, the verifier cannot evaluate both sides without the help of the prover! The left-hand side involves evaluations of the trace polynomials at the oods point (and potentially shifted oods points), and the right-hand side involves evaluations of the composition column polynomials at the oods point as well.
As such, the prover sends the needed evaluations to the verifier so that the verifier can perform the check. (These evaluations are often referred to as the "mask" values.)
Notice that this "oods check" cannot happen in the domain used to index the trace polynomials. This is because the left-hand side involves divisions by domain polynomials , which might lead to divisions by zero.
This is why the oods point is called "out-of-domain sampling". Although nothing special is done when sampling this point, but the probability that it ends up in the trace domain is very low.
TODO: explain what parts does the term "DEEP" refer to in this protocol.
Aggregation and FRI Proof
The verifier now has to:
- Perform a FRI check on (which will verify the original prover claim that the trace polynomials satisfy the constraints).
- Verify all the evaluations that were sent, the prover and the verifier can use FRI-PCS for that, as described in the FRI-PCS section of the Starknet FRI Verifier specification.
TODO: the second point also should have the effect of proving that the commitments to the trace column polynomials are correct (as they will also act as FRI checks)
In order to avoid running multiple instances of the FRI protocol, the FRI Aggregation technique is used as described in the Aggregating Multiple FRI Proofs section of the Starknet FRI Verifier specification. The verifier sends a challenge called oods_alpha which is used to aggregate all of the first layer of the previously discussed FRI proofs.
Finally, the FRI protocol is run as described in the Starknet FRI Verifier specification.