Static Lookups

In the previous section, we showed how to create a preprocessed trace. In this section, we will introduce the concept of an interaction trace, and use it with the preprocessed trace to implement static lookups.

Let's start with a brief introduction to lookups. A lookup is a way to connect values from one part of the table to another part of the table. A simple example is when we want to copy values across parts of the table. At first glance, this seems feasible using a constraint. For example, we can copy $co l_{1}$ values to $co l_{2}$ by creating a constraint that $co l_{1} - co l_{2}$ is equal to $0$ . The limitation with this approach, however, is that the same constraint needs to be satisfied over every row in the columns. In other words, we can only check that $co l_{2}$ is an exact copy of $co l_{1}$ :

$co l_{1} [i] = co l_{2} [i] \forall i$

But what if we want to check that $co l_{2}$ is a copy of $co l_{1}$ regardless of the order of the values? This can be done by comparing that the grand product of the random linear combinations of all values in $co l_{1}$ is equal to the grand product of the random linear combinations of all values in $co l_{2}$ :

$i = 0 \prod n - 1 (X - co l_{1} [i]) = i = 0 \prod n - 1 (X - co l_{2} [i])$

where $X$ is a random value from the verifier.

By taking the logarithmic derivative of each side of the equation, we can rewrite it:

$i = 0 \sum n - 1 \frac{1}{X - co l _{1} [ i ]} = i = 0 \sum n - 1 \frac{1}{X - co l _{2} [ i ]}$

We can go further and allow each of the original values to be copied a different number of times. This is supported by modifying the check to the following:

$i = 0 \sum n - 1 \frac{1}{X - co l _{1} [ i ]} = i = 0 \sum n - 1 \frac{m _{i}}{X - co l _{2} [ i ]}$

Where $m_{i}$ represents the multiplicity, or the number of times $co l_{1} [i]$ appears in $co l_{2}$ .

In Stwo, these fractions (which we will hereafter refer to as LogUp fractions) are stored in a special type of trace called an interaction trace. An interaction trace is used to contain values that involve interaction between the prover and the verifier. As mentioned above, a LogUp fraction requires a random value $X$ from the verifier, which is why it is stored in an interaction trace.

Range-check AIR

We will now walk through the implementation of a static lookup, which is a lookup where the values that are being looked up are static, i.e. part of the preprocessed trace. Specifically, we will implement a range-check AIR, which checks that a certain value is within a given range. This is especially useful for frameworks like Stwo that use finite fields because it allows checking for underflow and overflow.

A range-check checks that all values in a column are within a certain range. For example, as in Figure 1, we can check that all values in the range-checked columns are between 0 and 3. We do this by first creating a multiplicity column that counts the number of times each value in the preprocessed trace appears in the range-checked columns.

Then, we create two LogUp columns as part of the interaction trace. The first column contains in each row a fraction with numerator equal to the multiplicity and denominator equal to the random linear combination of the value in the range column. For example, for row 1, the fraction should be $\frac{2}{X - 0}$ , where $X$ is a random value. The second column contains batches of fractions where the denominator of each fraction is the random linear combination of the value in the range-checked column. Note that the numerator of each fraction is always -1, i.e. we apply a negation, because we want the sum of the first column to be equal to the sum of the second column.

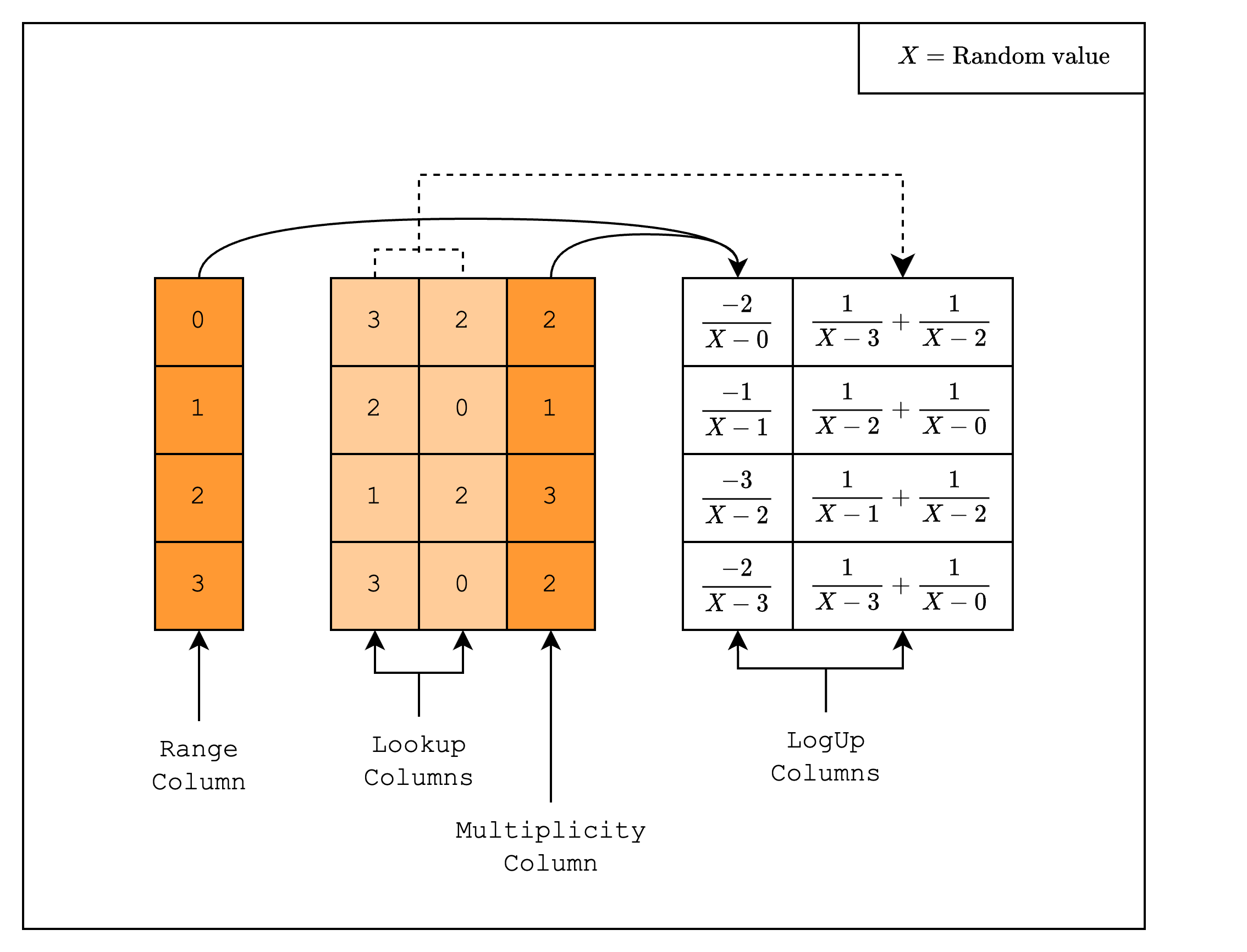
If we add all the fractions in the two columns together, we get 0. This means that the verifier will be convinced with high probability that the values in the range-checked columns are a subset of the values in the range column.

Implementation

Now let's move on to the implementation where we create a 4-bit range-check AIR. We do this by creating a preprocessed trace column with the integers $[0, 16)$ , then using a lookup to force the values in the original trace columns to lie in the values of the preprocessed column.

struct RangeCheckColumn {
    pub log_size: u32,
}

#[allow(dead_code)]
impl RangeCheckColumn {
    pub fn new(log_size: u32) -> Self {
        Self { log_size }
    }

    pub fn gen_column(&self) -> CircleEvaluation<SimdBackend, M31, BitReversedOrder> {
        let col = BaseColumn::from_iter((0..(1 << self.log_size)).map(|i| M31::from(i)));
        CircleEvaluation::new(CanonicCoset::new(self.log_size).circle_domain(), col)
    }

    pub fn id(&self) -> PreProcessedColumnId {
        PreProcessedColumnId {
            id: format!("range_check_{}_bits", self.log_size),
        }
    }
}

First, we need to create the range-check column as a preprocessed column. This should look familiar to the code from the previous section.

fn gen_trace(log_size: u32) -> Vec<CircleEvaluation<SimdBackend, M31, BitReversedOrder>> {
    // Create a table with random values
    let mut rng = rand::thread_rng();
    let lookup_col_1 =
        BaseColumn::from_iter((0..(1 << log_size)).map(|_| M31::from(rng.gen_range(0..16))));
    let lookup_col_2 =
        BaseColumn::from_iter((0..(1 << log_size)).map(|_| M31::from(rng.gen_range(0..16))));

    let mut multiplicity_col = BaseColumn::zeros(1 << log_size);
    lookup_col_1
        .as_slice()
        .iter()
        .chain(lookup_col_2.as_slice().iter())
        .for_each(|value| {
            let index = value.0 as usize;
            multiplicity_col.set(index, multiplicity_col.at(index) + M31::from(1));
        });

    // Convert table to trace polynomials
    let domain = CanonicCoset::new(log_size).circle_domain();
    vec![
        lookup_col_1.clone(),
        lookup_col_2.clone(),
        multiplicity_col.clone(),
    ]
    .into_iter()
    .map(|col| CircleEvaluation::new(domain, col))
    .collect()
}

Next, we create the original trace columns. The first two columns are random values in the range $[0, 15]$ , and the third column contains the counts of the values in the range-check column.

relation!(SmallerThan16Elements, 1);

fn gen_logup_trace(
    range_log_size: u32,
    log_size: u32,
    range_check_col: &BaseColumn,
    lookup_col_1: &BaseColumn,
    lookup_col_2: &BaseColumn,
    multiplicity_col: &BaseColumn,
    lookup_elements: &SmallerThan16Elements,
) -> (
    Vec<CircleEvaluation<SimdBackend, M31, BitReversedOrder>>,
    SecureField,
) {
    let mut logup_gen = LogupTraceGenerator::new(range_log_size);

    let mut col_gen = logup_gen.new_col();
    for simd_row in 0..(1 << (range_log_size - LOG_N_LANES)) {
        let numerator: PackedSecureField = PackedSecureField::from(multiplicity_col.data[simd_row]);
        let denom: PackedSecureField = lookup_elements.combine(&[range_check_col.data[simd_row]]);
        col_gen.write_frac(simd_row, -numerator, denom);
    }
    col_gen.finalize_col();

    let mut col_gen = logup_gen.new_col();
    for simd_row in 0..(1 << (log_size - LOG_N_LANES)) {
        let lookup_col_1_val: PackedSecureField =
            lookup_elements.combine(&[lookup_col_1.data[simd_row]]);
        let lookup_col_2_val: PackedSecureField =
            lookup_elements.combine(&[lookup_col_2.data[simd_row]]);
        // 1 / denom1 + 1 / denom2 = (denom1 + denom2) / (denom1 * denom2)
        let numerator = lookup_col_1_val + lookup_col_2_val;
        let denom = lookup_col_1_val * lookup_col_2_val;
        col_gen.write_frac(simd_row, numerator, denom);
    }
    col_gen.finalize_col();

    logup_gen.finalize_last()
}

fn main() {
    ...
    // Draw random elements to use when creating the random linear combination of lookup values in the LogUp columns
    let lookup_elements = SmallerThan16Elements::draw(channel);

    // Create and commit to the LogUp columns
    let (logup_cols, claimed_sum) = gen_logup_trace(
        range_log_size,
        log_num_rows,
        &range_check_col,
        &trace[0],
        &trace[1],
        &trace[2],
        &lookup_elements,
    );
    ...
}

Now we need to create the LogUp columns.

First, note that we are creating a SmallerThan16Elements instance using the macro relation!. This macro creates an API for performing random linear combinations. Under the hood, it creates two random values $z, α$ that can create a random linear combination of an arbitrary number of elements. In our case, we only need to combine one value (value in $[0, 15]$ ), which is why we pass in 1 to the macro.

Inside gen_logup_trace, we create a LogupTraceGenerator instance. This is a helper class that allows us to create LogUp columns. Every time we create a new column, we need to call new_col() on the LogupTraceGenerator instance.

You may notice that we are iterating over BaseColumn in chunks of 16, or 1 << LOG_N_LANES values. This is because we are using the SimdBackend, which runs 16 lanes simultaneously, so we need to preserve this structure. The Packed in PackedSecureField means that it packs 16 values into a single value.

You may also notice that we are using a SecureField instead of just the Field. This is because the random value we created by SmallerThan16Elements lies in the degree-4 extension field $F_{p^{4}}$ . This is necessary for the security of the protocol and interested readers can refer to the Mersenne Primes section for more details.

Once we set the fractions for each simd_row, we need to call finalize_col() to finalize the column. This process modifies the LogUp columns from individual fractions to cumulative sums of the fractions as shown in Figure 2.

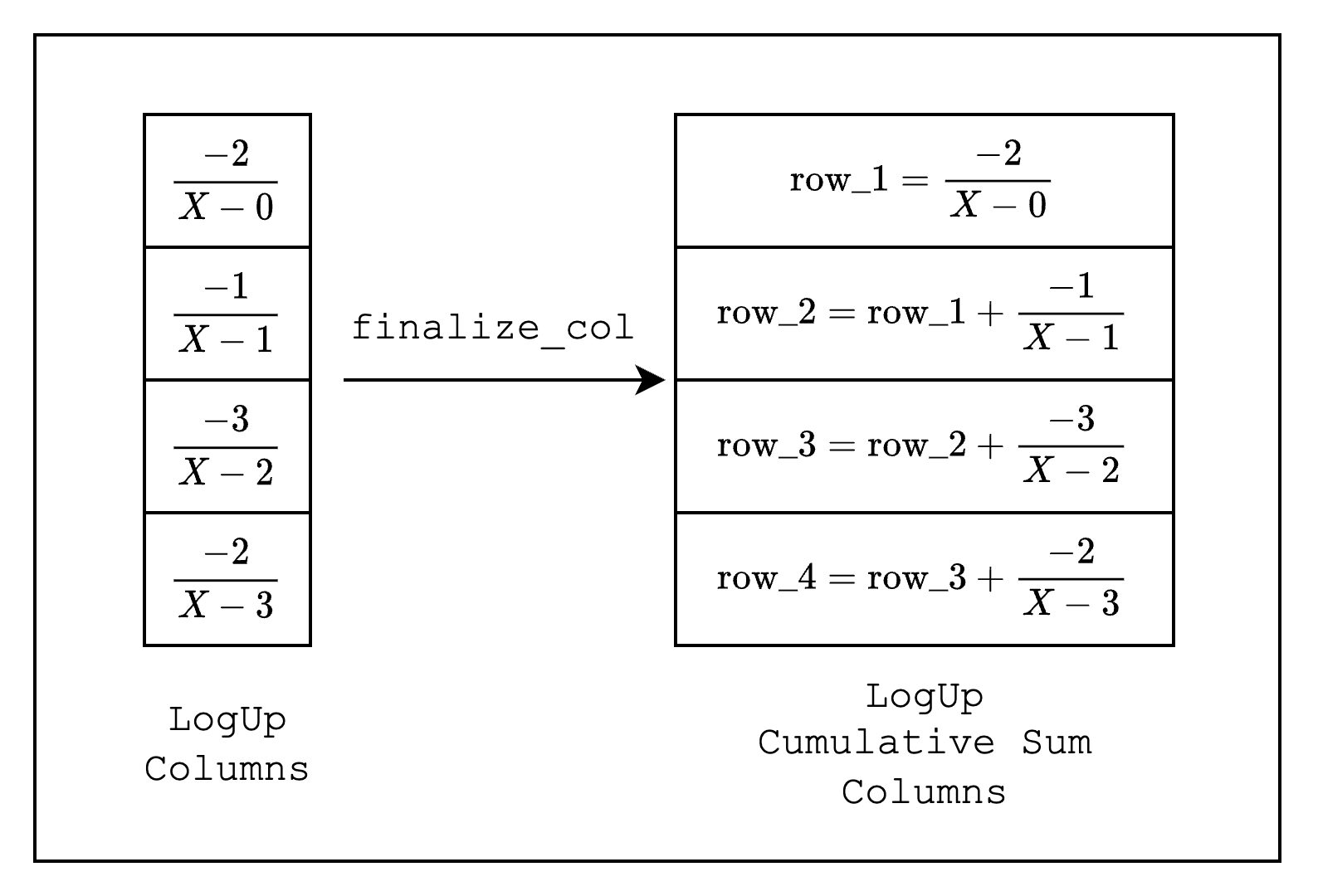
Finally, we need to call finalize_last() on the LogupTraceGenerator instance to finalize the LogUp columns, which will return the LogUp columns as well as the sum of the fractions in the LogUp columns.

struct TestEval {
    range_check_id: PreProcessedColumnId,
    log_size: u32,
    lookup_elements: SmallerThan16Elements,
}

impl FrameworkEval for TestEval {
    fn log_size(&self) -> u32 {
        self.log_size
    }

    fn max_constraint_log_degree_bound(&self) -> u32 {
        self.log_size + LOG_CONSTRAINT_EVAL_BLOWUP_FACTOR
    }

    fn evaluate<E: EvalAtRow>(&self, mut eval: E) -> E {
        let range_check_col = eval.get_preprocessed_column(self.range_check_id.clone());

        let lookup_col_1 = eval.next_trace_mask();
        let lookup_col_2 = eval.next_trace_mask();
        let multiplicity_col = eval.next_trace_mask();

        eval.add_to_relation(RelationEntry::new(
            &self.lookup_elements,
            -E::EF::from(multiplicity_col),
            &[range_check_col],
        ));

        eval.add_to_relation(RelationEntry::new(
            &self.lookup_elements,
            E::EF::one(),
            &[lookup_col_1],
        ));

        eval.add_to_relation(RelationEntry::new(
            &self.lookup_elements,
            E::EF::one(),
            &[lookup_col_2],
        ));

        eval.finalize_logup_batched(&vec![0, 1, 1]);

        eval
    }
}

The last piece of the puzzle is to create the constraints. We use the same TestEval struct as in the previous sections, but the evaluate function will look slightly different. Instead of calling add_constraint on the EvalAtRow instance, we will call add_to_relation, which recreates the fractions that we added in the LogUp columns using values in the range-check, lookup, and multiplicity columns.

Once we add the fractions as constraints, we call the finalize_logup_batched function, which indicates how we want to batch the fractions. In our case, we added 3 fractions but want to create batches where the last two fractions are batched together, so we pass in &vec![0, 1, 1].

    // Verify
    assert_eq!(claimed_sum, SecureField::zero());

    let channel = &mut Blake2sChannel::default();
    let commitment_scheme = &mut CommitmentSchemeVerifier::<Blake2sMerkleChannel>::new(config);
    let sizes = component.trace_log_degree_bounds();

    commitment_scheme.commit(proof.commitments[0], &sizes[0], channel);
    channel.mix_u64((log_num_rows) as u64);
    commitment_scheme.commit(proof.commitments[1], &sizes[1], channel);
    commitment_scheme.commit(proof.commitments[2], &sizes[2], channel);

    verify(&[&component], channel, commitment_scheme, proof).unwrap();

When we verify the proof, as promised, we check that the claimed_sum, which is the sum of the fractions in the LogUp columns, is 0.

And that's it! We have successfully created a static lookup for a range-check.

Note

How many fractions can we batch together?

This depends on how we set the max_constraint_log_degree_bound function, as discussed in this note. More specifically, we can batch up to exactly the blowup factor.

e.g.

self.log_size + 1 -> 2 fractions
self.log_size + 2 -> 4 fractions
self.log_size + 3 -> 8 fractions
self.log_size + 4 -> 16 fractions
...

Note

Note that unlike what Figure 1 shows, the size of the range column and the range-checked columns do not have to be the same. As we will learn in the Components section, we can create separate components for the range-check and the range-checked columns to support such cases.

Stwo Book

Static Lookups

Range-check AIR

Implementation