Proving and Verifying an AIR

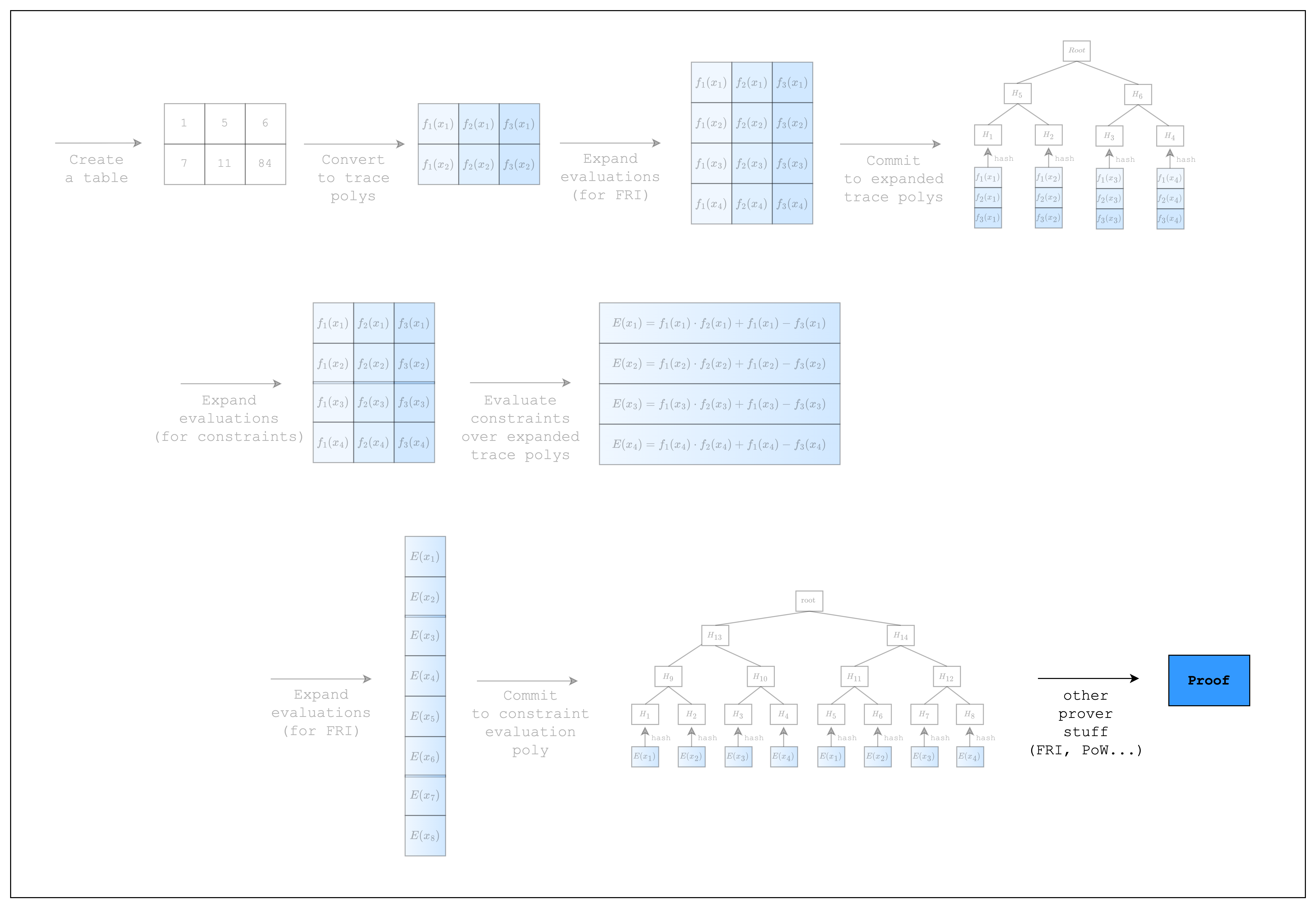
We're finally ready for the last step: prove and verify an AIR!

Since the code is relatively short, let us present it first and then go over the details.

fn main() {
    // --snip--

    // Prove
    let proof = prove(&[&component], channel, commitment_scheme).unwrap();

    // Verify
    let channel = &mut Blake2sChannel::default();
    let commitment_scheme = &mut CommitmentSchemeVerifier::<Blake2sMerkleChannel>::new(config);
    let sizes = component.trace_log_degree_bounds();

    commitment_scheme.commit(proof.commitments[0], &sizes[0], channel);
    channel.mix_u64(log_num_rows as u64);
    commitment_scheme.commit(proof.commitments[1], &sizes[1], channel);

    verify(&[&component], channel, commitment_scheme, proof).unwrap();
}

Prove

As you can see, there is only a single line of code added to create the proof. The prove function performs the FRI and PoW operations under the hood, although, technically, the constraint-related steps in Figure 1 were not performed in the previous section and are only performed once prove is called.

Verify

In order to verify our proof, we need to check that the constraints are satisfied using the commitments from the proof. In order to do that, we need to set up a Blake2sChannel and CommitmentSchemeVerifier<Blake2sMerkleChannel>, along with the same PcsConfig that we used when creating the proof. Then, we need to recreate the Fiat-Shamir channel by passing the Merkle tree commitments and the log_num_rows to the CommitmentSchemeVerifier instance by calling commit (remember: the order is important!). Then, we can verify the proof using the verify function.

Congratulations! We have come full circle. We now know how to create a table, convert it to trace polynomials, commit to them, create constraints over the trace polynomials, and prove and verify the constraints (i.e. an AIR). In the following sections, we will go over some more complicated AIRs to explain Stwo's other features.