Writing a Spreadsheet
In order to write a proof, we first need to create a table of rows and columns. This is no different from writing integers to an Excel spreadsheet as we can see in Figure 2.
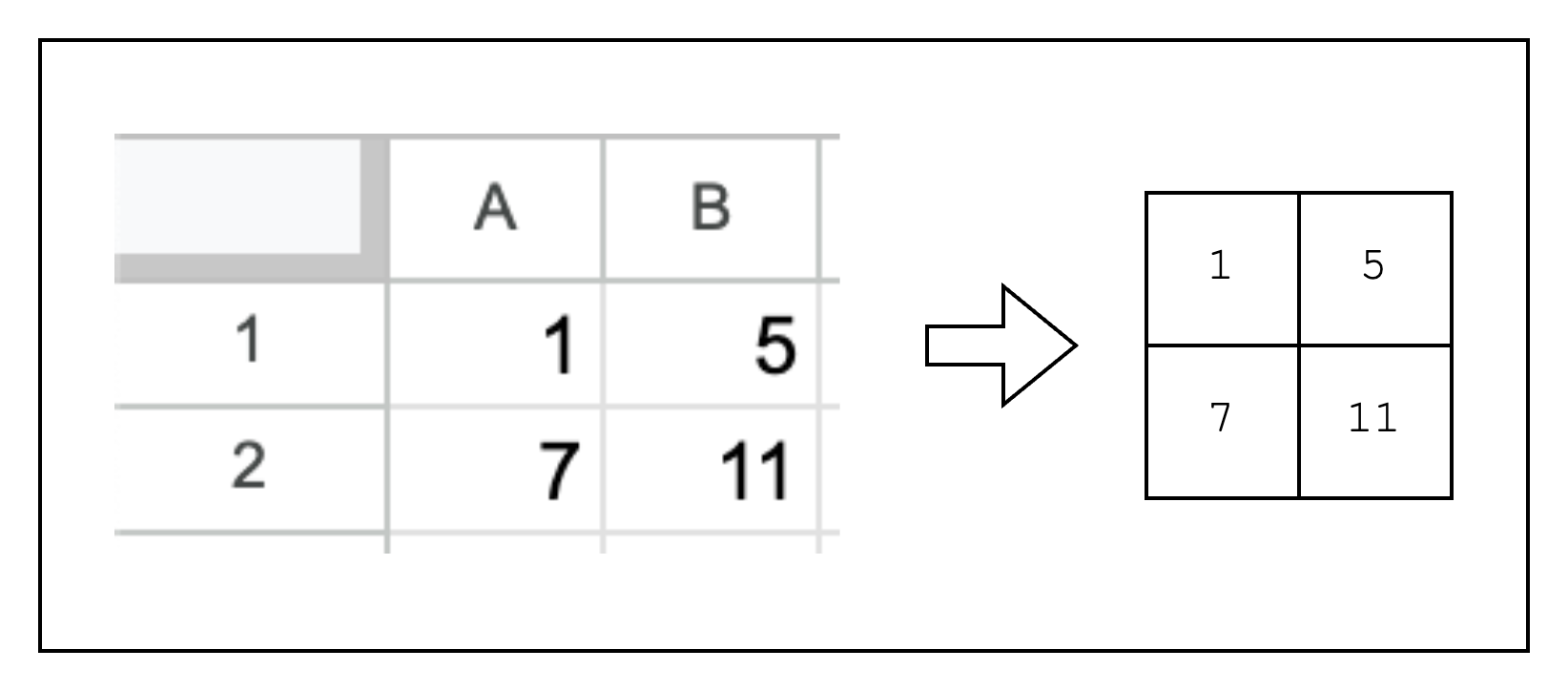
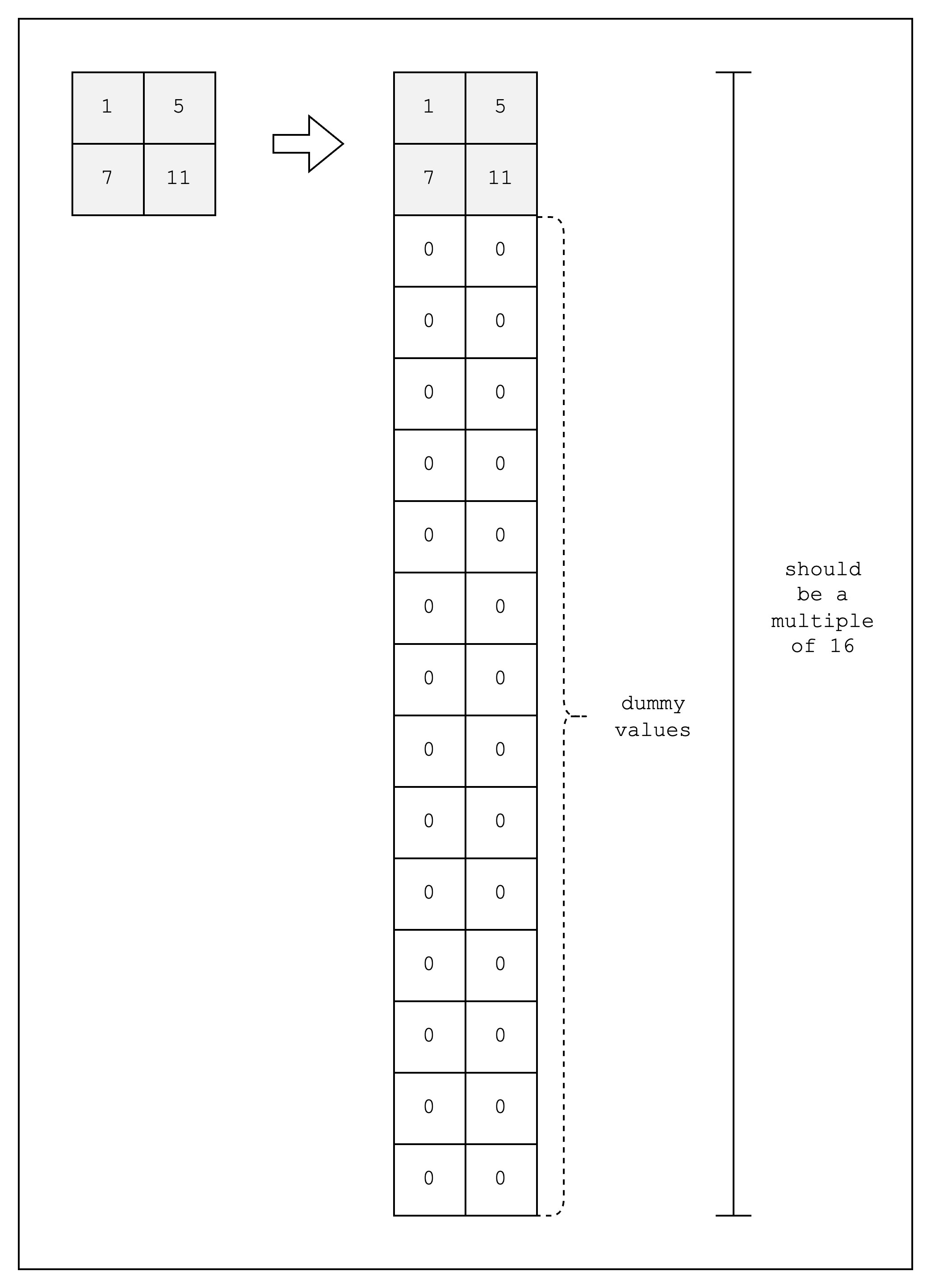
But there is a slight caveat to consider when creating the table. Stwo implements SIMD operations to speed up the prover in the CPU, but this requires providing the table cells in chunks of 16 rows. Simply put, this is because Stwo supports 16 lanes of 32-bit integers, which means that the same instruction can be run simultaneously for 16 different data.
Alas, for our table, we will need to create 14 dummy rows to make the total number of rows equal to 16, as shown in Figure 3. For the sake of simplicity, however, we will omit the dummy rows in the diagrams of the following sections.
Given all that, let's create this table using Stwo.
use stwo::prover::{
backend::{
simd::{column::BaseColumn, m31::N_LANES},
Column,
},
};
use stwo::core::fields::m31::M31;
fn main() {
let num_rows = N_LANES;
let mut col_1 = BaseColumn::zeros(num_rows as usize);
col_1.set(0, M31::from(1));
col_1.set(1, M31::from(7));
let mut col_2 = BaseColumn::zeros(num_rows as usize);
col_2.set(0, M31::from(5));
col_2.set(1, M31::from(11));
}As mentioned above, we instantiate the num_rows of our table as N_LANES=16 to accommodate SIMD operations. Then we create a BaseColumn of N_LANES=16 rows for each column and populate the first two rows with our values and the rest with dummy values.
Note that the values in the BaseColumn need to be of type M31, which refers to the Mersenne-31 prime field that Stwo uses. This means that the integers in the table must lie in the range .
Now that we have our table, let's move on!